AIST/HQL人体寸法・形状データベース2003-相同モデルの統計的分析

３．多次元尺度法による個人差の分析

３－１．変異軸とその解釈

　2つの相同モデル間の距離（非類似度）を定義し、N個の相同モデル間の距離行列を多次元尺度法で分析することにより、変異軸と散布図を取得することができます。三角形の３辺の長さが分かれば、３つの頂点の位置関係を２次元の散布図で表現することができます。同様に、多次元尺度法ではN個の相同モデル間の距離関係をできるだけよく再現するように変異軸（尺度）と得点を決定します。このとき、点間のばらつきが最大になるように第１軸を定めます。第２軸以下は、それより上位の軸とは無相関で、かつばらつきが最大になるように定めます。サイズの個人差がどの程度大きいかに依存しますが、人体の相同モデルの場合4～5個の軸で距離行列のもつ情報の80%以上を説明できることが多いようです。

　相同モデルを分析した例として、多次元尺度法を用いて今回公開した男性47体の相同モデルの形態変異を分析した結果を紹介します。身長の違い、立ったときの姿勢の違いによって、47体の相同モデルの空間内の位置にはばらつきがあります。そこで、腸骨稜点のレベルにおける断面に上下方向位置をそろえ（腸骨稜点のレベルがZ＝０）、このレベルの断面の前後径の中心に前後方向位置をそろえてから分析をしました（腸骨稜レベル断面の前後の中心がX＝０）（図１）。すべてのモデルをこのように定義された人体座標系で記述してあります。

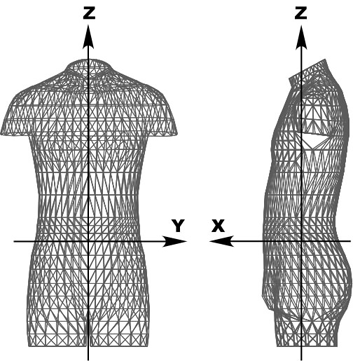図１．座標系

　対応するデータ点間の距離の総和として形態間距離を定義し、多次元尺度法（HBS使用）を用いて距離行列を分析しました。この結果、5つの変異軸で距離行列のもつ情報の96％が説明されました。各軸がどのような個人差を表しているかは、その軸の得点が非常に高いサンプルと非常に低いサンプルを比べることにより解釈することができます。ここでは、HBSを使って各軸の得点が±3標準偏差の位置にある仮想形状を計算し、軸を解釈しました：

• 第１軸：体幹部のサイズ。幅
• 第２軸：背なかの反り具合
• 第３軸：太り具合
• 第４軸：背すじの湾曲の強さ
• 第５軸：姿勢のばらつき：左右への傾きと上半身のねじれ

３-２．散布図

　各軸の得点は正規分布をしていました。したがって、多次元尺度法で得られた変異軸上の得点として３次元形状の情報を要約し、統計的に扱う事ができるようになります。図２は第２軸と第３軸の得点に基づいて描いた散布図です。この散布図の分布の中心にあるのが、４つの軸の得点すべてが０である平均形状です。散布図上で、各軸の端にある、たとえば得点の標準偏差を計算し、±3標準偏差の位置にある形状や、第１軸と第２軸の得点を使って被験者の95％がその中にはいるような確率楕円上にある形状などを計算することができれば、３次元形状の分布の範囲を直感的に知ることができます。

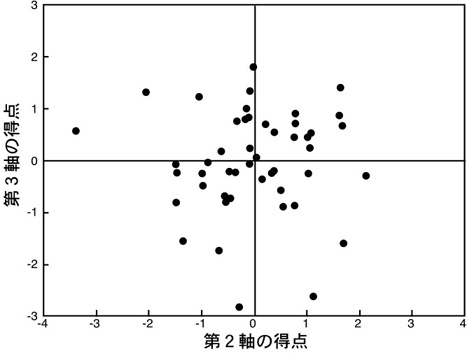図２．散布図の例

３-３．分布図上の任意の位置にある仮想形状の計算

軸上の仮想形状は、以下の方法で計算することができます：

1. MDS得点に基づく分布の中心付近、たとえば±1標準偏差の範囲にある仮想形状を10個程度、実際の形状の重みつき和として算出します（ただし、重み＞0）。
2. 分布の中心にある平均形状を初期形態としてこの周囲に制御格子点を定義し、平均形状を1.で計算した複数の仮想形状それぞれに変換するFFD (Free Form Deformation) の格子ひずみを計算します。なお、平均形状は全データの平均値として簡単に計算することができます。
3. 2.で計算した変形格子の制御格子点それぞれにつき、軸の座標値（MDS得点）と制御格子点の動きの関係を回帰式で表します。両者の相関関係は、通常非常に強い（相関係数は0.95以上）。
4. 分布軸上の任意の点、たとえば座標値（x1, 0 , 0, 0）をもつ点、に位置する形状モデルを計算するための変形格子を、3.で計算した回帰式を用いて計算します。
5. 4.で求めた変形格子を用いて平均形状モデルを変換することにより、求める仮想形状を計算できます。
   分布図上の任意の点と原点を通る直線を想定し、この直線上の仮想形状を重み付き平均で求めることにより、上記の方法で分布図上の任意の位置にある仮想形状を計算することができます。
   図３は上記の方法で平均形状と第２、第３軸上で±3標準偏差の位置にある仮想形状を計算したものです。体形の個人差は、全体的な大きさや太り具合だけでなく、背なかの反り具合や背すじの湾曲など、姿勢に関連した個人差も大きいことがわかります。

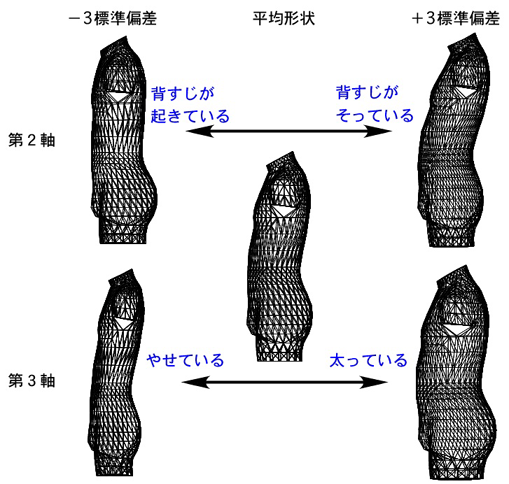図３．第２軸、第３軸上の仮想形状。左は3標準偏差、中央は平均、右は＋3標準偏差の位置にある形状

４．分析用ソフトウェア

４-１．多次元尺度法

　多次元尺度法はSPSSなど市販の統計計算パッケージに入っていますが、変量の数あるいはサンプル数に制限があり、サンプル数が多い場合は市販のソフトが使えないことがあります。また、上記の方法で仮想形状を計算するためにはFree Form Deformation（FFD）法により平均形状モデルを仮想形状の相同に変換するための制御格子点の移動量を計算し、さらに格子点の数だけ直線回帰式を計算しなければなりません。

　これらの計算は非常に手間がかかるので、デジタルヒューマン研究センターでは、N個の相同モデルから距離行列を計算し、多次元尺度法で分析して散布図を作成し、分布図上の任意の位置にある仮想形状を計算するソフトウェア、HBS(Human Body Statistica)を開発しました。このソフトは産総研ベンチャーであるデジタルヒューマンテクノロジー社より販売しています。このソフトウェアを使用するうえで、サンプル数は200以下という制限がありますが、相同モデルのデータ点数に制限はありません。ただし、データ点数がふえるとFFDの変形格子の計算時間が長くなります。

４-２．主成分分析法

　図１のような相同モデルがN個あれば、全データ点のｘ、ｙ、ｚ座標値を用いて主成分分析を行い、情報圧縮をするとともに個人差の大きな変異軸を取得し、主成分得点を用いてN個の相同モデルの散布図を描くことができます。主成分分析法によれば、任意の主成分得点の組をもつ仮想形状を算出することもできます。この方法は、相同モデルが図１に示した例よりももっと詳細で、データ点数が多い場合、有効です。

　座標値を用いて主成分分析を行う場合、変数の数は非常に大きくなります。このため、市販の統計計算パッケージにはいっている主成分分析法のプログラムは分析できる変数の数に制限があるために使えないことがあります。上述したデジタルヒューマン研究センターで開発されたソフトウェアHBS(Human Body Statistica)は、主成分分析法により形状モデルを分析するオプションがふくまれています。ただし、変数の数（データ点数×3）には15000以下という制限があります。データ点数が多いと、計算時間は長くなります。

４-３．多次元尺度法と主成分分析法の得失

　HBS(Human Body Statistica)には多次元尺度法で形態間距離行列を分析するオプションと、主成分分析法でモデルの座標値を分析するオプションがあります。両者の結果は当然ながら、必ずしも一致しません。

　多次元尺度法の長所は情報圧縮効率が高い点です。相同モデルのデータ点数が数100～1000個程度の場合、多次元尺度法では4～5個の尺度でもとの距離行列がもつ情報の80％以上を説明できることが多いようです。これに対して、主成分分析をすると80％程度の情報を説明するために、十数個から20個程度の主成分が必要になることが多いようです。主成分分析法の長所は、分布の任意の位置にある形状の再現が容易なことです。

５．文献

• Mochimaru, M., M. Kouchi, and M. Dohi, 2000: Analysis of 3-D human foot forms using the Free Form Deformaiotn method and its application in grading shoe lasts. Ergonomics, 43(9): 1301-1333.
• Mochimaru, M. and M. Kouchi, 2000: Statistics for 3D body forms. SAE Technical Paper, 2000-01-2149.
• Kouchi, M. and M. Mochimaru, 2004: Analysis of 3D face forms for proper sizing and CAD of spectacle frames. Ergnomics, 47:1499-1516.
• Kouchi, M. and M. Mochimaru, 2006: Inter-individual variations in intra-individual shape change patterns. SAE Technical Paper 2006-01-2353.

▲ ページトップへ