(関口智嗣委員)
21世紀の高度情報化時代のキーテクノロジーである基盤ソフトウエアにおいて我が国は大きく立ち遅れている。とりわけ、産業界における製品設計開発、製造、研究開発などの目的でさまざまに用いられている共通の知的資産としてのソフトウエア技術(以下、産業基盤ソフトウエア技術と呼ぶ)の大部分は海外の特定の製品に大きく依存している。具体的には、情報処理産業のみならず、新機能材料、半導体設計、新エネルギー開発、地球環境対策、資源探索、機械設計、防災計画などの分野で用いられている産業基盤ソフトウエアはその源流が欧米に発するものが多い。このような現状は、欧米各国から「科学技術タダ乗り」との非難を浴びると同時に、将来、わが国の産業競争力の著しい低下を招くものであり、早急に対策を講じる必要がある。このような産業基盤ソフトウエアや米国のHPCC計画グランドチャレンジに代表されるような大規模科学技術計算問題は今後ますます超高速スーパーコンピュータ、大規模データベース、広帯域高速ネットワークを最大限に活用して解く必要となってくる。したがって、こうしたソフトウエア技術がペタフロップスコンピューティングの発展を強く推進するニーズとなる。計算能力の観点からだけでも大雑把に1,000ギガフロップスから100,000ギガフロップス以上の能力がアプリケーションをより高精度に、より大規模に、より高速性が要求される。ペタフロップス(1,000,000ギガフロップス)の演算能力はインターネットに接続されているPCの総演算能力の数倍程度であり、また最高速の超並列計算機の1000倍程度に相当する。このように現状の技術の単なる延長上ではペタフロップスコンピューティングは実現されない。ここでは、アプリケーションを実行する観点からペタフロップスを実現する構成を 1)単体性能 2)並列度 3)ネットワークの3点から仮定を導入する。さらに、アプリケーションの実例として日本で計画中のVRMS(Virtual Microscope)を例にとり、ペタフロップスコンピューティングでの実現方法と展望について述べる。
単体プロセッサはすでにその能力の限界が来ていると言われる。しかし、半導体製造技術の革新により21世紀には1GIPSのマイクロプロセッサが実現すると言われている(本委員会ヒアリング資料を参照)。これをペタフロップスシステムの基本コンポーネントとする。基本コンポーネントに付加する専用ハードウエア加速装置はアプリケーションをある程度特定することで、実現することが可能である。従来の高速計算システム発展の歴史を見てみると、汎用機に付加した IAP (アレイプロセッサ)、これを一般化したベクトルパイプライン、FPS社などから提供されたミニコンピュータ用の加速装置、CM-5等で採用されたマイクロベクトルプロセッサ、最近ではGRAPEなどに代表される超高速な専用加速演算装置がある。これらは従来の汎用プロセッサと比較して10倍以上の能力があり、ペタフロップスを達成するための基本コンポーネントに不可欠なものである。ここでは、10ギガフロップスの専用ハードウエアを付加した1GIPSの汎用プロセッサという2ユニットを基本として単体の演算装置を構成する。
並列度についてはコネクタ、ケーブル等に起因する物理的な制約、相互結合ネットワークトポロジの制約、容易なプログラミング環境の提供等の条件から現状に対してさほど今後の技術発展が期待できない。もちろん、相互結合ネットワークに要求されるネットワークスループットは現状の10倍程度以上は必要となる。ここでは、Hitachi SR2201等ですでに実績のある1,024台程度で3次元クロスバという構成の相互接続が可能であると仮定する。
上記2つの条件は単体プロセッサならびに相互結合ネットワークから構成される超並列システムに関するものである。すなわち単体のシステムの限界が 10ギガフロップスを1,024台で並列システムとして構成することにより約10テラフロップスを実現するというものである。しかし、これではまだペタフロップスには到達しない。そこで、この不足分を補うためには10テラフロップス級規模のシステムを100台規模高速ネットワークで接続したネットワークコンピューティングで解決する。現時点では32台から64台規模の構内ネットワークコンピューティングが現実的であるが、100台規模の広域分散コンピューティング環境を実現するためには
といった点の技術開発が必要であるが不可能な数字ではない。
以上をまとめて、スカラプロセッサ1GIPS+専用ハードウエア加速装置10ギガフロップス、これを1,024台並列のシステム(10テラフロップス)を100台程度のネットワークコンピューティングにより1ペタフロップスを実現することをこの章での仮定とする。
上記仮定においてネットワークコンピューティング技術開発がますます重要となるであろう。国内における高速ネットワーク技術の応用は従来マルチメディア利用技術として開発が実施されてきたため、HPCC技術に発展するようなネットワーク技術は、特に日本の技術が後れている。ネットワークコンピューティングとは高速ネットワークにより接続された計算機資源や計算資源を駆使することにより、それぞれの資源の物理的な位置を意識することなく従来単独では実行不可能であった情報処理を実現する技術である。
ネットワークコンピューティングの対象としては超高速数値処理を目指した技術と超大規模データ処理を目指した技術がある。すなわち、前者はスーパーコンピュータ、並列計算機システムといった高速計算機資源を有機的に連携して利用し、大規模なシミュレーションを実現する。後者はそれぞれが100GB程度のデータベースがシステム全体で1TB以上級のデータに対して処理を実施するものである。超高速数値処理アプリケーション技術としては例えば地球環境のシミュレーションでは海洋循環モデル、大気循環モデル、極地モデル、大陸モデル、化学反応モデル等を個別に高速計算機に分配し、これらを統合するためのカプリングモデルを導入しシミュレーションを実施する。現状の技術ではスーパーコンピュータを用いてもモデル単独を処理する程度が実用的である。精度の高い計算、長い時間軸に添った計算を行うにはネットワークで接続された高性能計算機の利用技術が必須である。また次節で述べるバーチャルマイクロスコープにおいても同様である。超大規模データ処理アプリケーション技術としてはDigital Sky Surveyとして天体観測データをデータベースとして保持し、世界中の研究者が各地のデータにアクセスすることで処理を行うものである。また、合成開口レーダの実時間データ処理などがあり、今後データ量はまさに天文学的数字となる。ネットワーク利用基盤技術としてはギガビットネットワークにおけるプロトコルとサーバの構築、ユーザが利用するクライアントライブラリ開発、ネットワークコンピューティングを記述するための言語開発、遠隔データベースへのアクセス技術開発、負荷分散と可用性、信頼性向上技術開発などがあげられる。
専用加速装置、超並列システム、ネットワークコンピューティングから構成されるペタフロップスコンピューティングシステムにおける想定されるアプリケーションとしてバーチャルマイクロスコープを実例として述べる。
(1)バーチャルマイクロスコープ全体概要
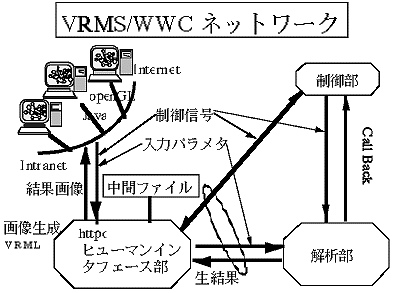
バーチャルマイクロスコープとは次のようなシステムである。分子軌道法と分子動力学法によれば、2つの方法を結合することにより、実験情報を全く使用せずに分子や原子の化学的振る舞いをシミュレーションすることが原理的に可能である。このような手法を用い化学プロセスをコンピュータ上で実現し、コンピュータグラフィックスで視覚化することにより、実験では観察不可能な化学現象をあたかも“顕微鏡”で見ているように観察することが可能である。このような、分子化学総合システムをバーチャルマイクロスコープと呼ぶこととする。このようなシステムは世界的に研究段階にあり、その実現に必要な技術は確立していない。さらに、本システムの特徴としては並列処理、分散処理、オブジェクト指向ソフトウエアなどの計算機技術の向上を十分に取り込んで開発を行うため、ライフタイムの長いソフトウエアとなることが期待されている。このバーチャルマイクロスコープ・システムは、バーチャルマイクロスコープ制御部、ヒューマンインタフェース部、解析部より構成される(図1)。

(2)バーチャルマイクロスコープ制御部
バーチャルマイクロスコープ制御部は、システム全体をバーチャルマイクロスコープとして機能させるための制御部であり、ヒューマンインタフェース部と解析部との動作を整合・制御する機能、ヒューマンインタフェース部と解析部とのデータの流れを制御する機能、計算結果をリアルタイムで表示するための解析部を制御する機能を有する。これらの機能を実現するためには、それぞれ、イベントの制御技術、データの流れの制御技術、人間の認知時間での表示技術が不可欠である。現象を追跡しながら、ある時点で現象をゆるやかに進行させたり、時間を戻したりするなどのロールバックが必要となったり、ある時点で解像度を変えて再計算を行ったり、観測・認識したい現象の呈示手法を即時に変更したり、さまざまな要求が解析部とヒューマンインタフェース部の相互を往復する。
(3)ヒューマンインタフェース部
ヒューマンインタフェース部は、解析条件の入力、分子構造の作成および分子構造と計算結果の物理量(電子密度分布の時間変化等)の表示を行う。分子構造の作成や分子構造の表示を対話的に行い、必要な情報(計算結果、分子構造等)を、必要な形態(3次元グラフィックス、グラフ、2次元グラフィックス、数値等)で、必要なときに表示する。これにより、あたかも実際の顕微鏡を操作する感覚で、実際には観察不可能な物理量を観察可能とする。
(4)バーチャルマイクロスコープ解析部
解析部は、第一原理分子動力学法を中心とした計算システムである。この計算システムは、分子軌道法の中で、分子の安定構造の予測など基底状態の計算に有効であるSCF法と密度汎関数法から構成される。いずれも電子の波動関数を求めるHartree-Fock法と原子核の安定位置を求めるエネルギー勾配法からなる。第一原理分子動力学法は、エネルギー勾配法により計算された原子核に働く力を用い、分子動力学により、化学反応における電子分布および分子骨格の経時的変化を計算する。原子核に働く力を第一原理計算で求め、分子動力学法により時間変化を計算する技術は世界的にも研究段階にあり、実現していない。
(5)ペタフロップスシステムでの実現
バーチャルマイクロスコープの各部はそれぞれに大規模計算を必要とする。特に解析部は現在のスーパーコンピュータ(SX−4)においても1,000軌道程度の計算を実現するのに数時間を要する。実用的には数万軌道の計算を数秒の単位で実現することが可能でないとあたかも顕微鏡を見るようにバーチャルマイクロスコープを実現することはできない。2電子積分と呼ばれる主たる計算部分の計算時間は基底数の4乗のオーダに比例する。ところが逆にこの部分は専用ハードウエア化が可能でもある。したがって、計算能力で約100,000倍以上が求められるので100ギガフロップスが要求される。これはネットワークコンピューティングにおいて10ギガフロップス級のシステムを10台程度接続することを意味する。各構成部は高速ネットワークにより接続され、制御データ、解析部からの生データ、入力パラメータ等がやりとりされる。さらに出力として生成されたグラフは現状技術で言うところのOpenGLやVRML、Javaのようネットワークコンピューティングと密接に関連した技術を通じて共有可能となる。こうしたことからもバーチャルマイクロスコープ技術の延長上に先に述べたペタフロップスシステムが適合することが期待される。
(中島克人委員)
進歩の早い情報処理関係の技術および市場の予測をするのに、20年後の議論は困難であり、徒労に帰する確率が高いので、ここではおよそ10年後ぐらいのレンジで、ペタフロップスマシン(またはペタフロップススケールのマシン、以後同様)の未来を予想することにする。このレンジで議論する限り、ペタフロップスマシンは少なくとも「高価で稀少なマシン」という位置付けで捉えられ、例えば「身近なPCが全てペタフロップス」という想定は除外される。というのは、ペタフロップスマシンの実現は専用のものでも5年以上[1]、汎用では20年かかる[2]と予想されているからである。
さて、10年後でさえも「高価で稀少なマシン」であるペタフロップスマシンの開発について、米国は早くも検討を開始しているのであるが、これを我々はどう見れば良いであろうか?
ピラミッド説
エジプトの巨大ピラミッドの建造理由は王権の強化のためと言われている。圧倒的な国王の威厳の象徴であるばかりでなく、当時の最新の建造技術とその建造を整然と遂行させる強固な中央集権組織のデモンストレーションでもあったと想像されている。しかし、建造後のピラミッド自身は(当時許されたかどうかは定かではないが)物見櫓程度にしか使えず、主に「王権のシンボル」という無形の精神作用のためだけのものとなる。国家財政を破綻させかねないような莫大な建造費用と年月をかけるピラミッド建造が何百年も続けられたということは、その精神作用にそれだけの価値があったわけである。
ペタフロップスマシンとは米国科学技術の優位性を象徴するためだけのピラミッドなのであろうか?
宇宙開発説
1960年代にソ連と米国による宇宙開発競争が繰り広げられた。莫大な国家予算をつぎ込むことができた理由は幾つかあろう。冷戦時代における兵器開発競争が第1の理由に違いない。しかし、ピラミッドと同様、国家威信をかけた面も大きかったと見られる。ピラミッドの場合と(恐らく)異なるのは、民衆が宇宙開発の結果に夢を持てたことであろう。宇宙旅行や地球外生命との遭遇等のロマン(?)の実現以外に、実利として、地球外資源の獲得、新材料の発見・開発、地球外植民地の開発などの夢があったはずである。
しかし、1969年に月への有人飛行が実現して30年近く経たというのに、宇宙開発は当初想像されたようなスピードでは進んでいない。1960年代のペースで開発が進めば、今日では火星への有人旅行ぐらいは(着陸できるかどうかは別問題として)できているような気がする。開発ペースが落ちたのは、もちろん冷戦の終結という理由もあったが、それ以前に、その膨大な予算を支えるだけの経済力と世論の支持が続かなかったからと言える。しかし、大きな夢やロマンの早期実現を諦めたかに見える傍ら、スペースシャトルを活用した実利を目指した宇宙開発はそれなりに進展した。また、人工衛星打ち上げが商用ベースに乗り、通信衛星の静止軌道上での場所争いに発展しそうなほど、宇宙利用は急速に伸びている。ペタフロップスマシンは米国科学技術の裾野を広げるための戦略的先陣部隊なのであろうか?
米国でのペタフロップスマシン開発の動きを、筆者は後者の宇宙開発を小規模にしたものと見るべきだと考える。ペタフロップスマシンの開発費は宇宙開発に比べれば恐らく「無視できるぐらいに小さい」であろうから、米国にとっては大々的に世論の支持を取りつける必要はなかろう。ただ、スポンサー(例えば米国DOEなどの省庁)がその投資に対して周囲の理解を得られるだけの理由を提示できればよい。冒険を許容し、欠点よりも長所を重視する米国の国民性ゆえ、ペタフロップスマシンの社会的貢献に期待をかけて、意外とスムーズに開発が進む可能性がある。
日本国民は技術開発に関して、かなり保守的であるといえよう。日本の宇宙開発の立ち遅れをペタフロップスマシンに当てはめると、日本が米国のペタフロップスマシン開発を愚行であると嘲笑している間に、その陰でテラフロップス級のマシンの利用とその技術を米国が蓄積し、わが国はますます米国と地力の差をつけられてしまうというシナリオも考えられなくもない。
以上、ペタフロップスマシン開発の政治的もしくは社会的な目的や位置付けを考察したが、どのような開発も現在もしくは将来のニーズ(=応用問題)の無い所に成果はあり得ない。以降では、ペタフロップスマシンが活かされるであろう応用問題に関する分析を試みる。
まずはアーキテクチャ、具体的にはPE(Processing Element)間通信コスト(レイテンシおよびバンド幅)が、ペタフロップス級の並列処理への適不適という意味で応用問題を選別するのではないかという仮説に基づき考察する。というのは、プロセッサ間がどんなに離れていても、「通信コストは一定である」ということは物理的に考えられないからである。
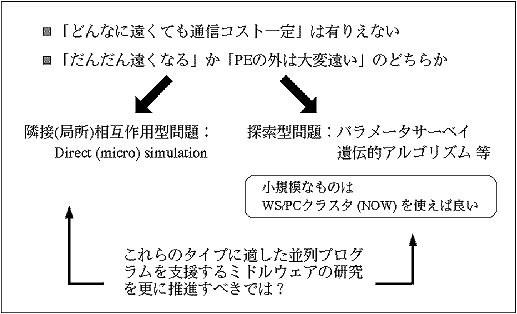
システムの直径が数十を超える並列マシンのPE間通信に関して、大きく分けて次の2つのどちらかに分類されると筆者は考える。
●「だんだん遠くなる」
システム内の隣接PE間では通信は速いが、遠方のPEとはその距離に応じて通信コストが大きくなると考える。多段バス結合に代表されるように、小システムを束ねて階層的に大きなシステムにまとめられたものはこの範疇と見なす。
このようなマシンモデルに適する応用問題の代表的な『タイプ』としてDirect (micro) simulation のような隣接(局所)相互作用を扱うものが挙げられる。プロセッサの隣接性と問題空間の隣接性を対応させるべきであることはいうまでもない。なお、N体問題に対する有名なBarnes-Hutアルゴリズムは、本来は大域的な通信と計算が頻繁に必要になる所を、それらを隣接相互作用問題に近い計算オーダに下げたという意義があり、このタイプに属するものとして考えることができる。
●「PEの外は大変遠い」
PE内にも厳密には1次キャッシュ、2次キャッシュ、主記億などの多段のメモリ階層があるが、PE内のデータアクセスに比べてPE間の通信コストがはっきりとした段差を感じさせる程大きい場合である。ノード内を共有メモリバス結合、ノード間をメッセージ通信ネットワークで接続した場合のノード内外の通信コストの違いはこの範疇と見なす。
こちらの場合は、計算間の同期頻度が非常に少なく済む代表的な『タイプ』として、探索型問題が挙げられる。工学的応用としては最適設計のためのパラメータの組合せを多数回のシミュレーションから求めるパラメータサーベイが代表例である。パラメータの組合せだけのデータ並列性があり、総当り、遺伝的アルゴリズム(例えば島モデル並列)、シミュレーティッド・アニ─リング(例えば温度並列)、ランダムウォーク(例えば方向並列)等、種々の並列化可能なアルゴリズムが存在する。
なお、このタイプの問題においては、その問題規模が小さい場合にはワークステーション(WS)やPCをLANで接続したようなWSクラスタやPCクラスタでも十分であることが多く、専用並列マシンに対するコストパフォーマンス上の強敵となる。
さて、これらのペタフロップス・スケールのマシンに期待がかかる問題の『タイプ』に対して、その並列プログラミングや並列実行を適切にサポートする基盤的、共通的ソフトウエア技術が健全に発展しているであろうか?
「PEの外は大変遠い」場合に関しては、WS/PCクラスタを1つの並列システムと見なしての、バッチジョブモニタに相当するツールの研究[3]やその製品化[4][5]などがすでに相当数見受けられる。探索型の用途に限定しなければ、LANまたはWAN上に分散された科学技術計算ライブラリを使い分けるシステム[6][7]なども現れつつあり、実用化も進みつつある。しかし、ユーザから見た場合の標準化や情報共有といった面ではそれぞれがバラバラの状態と言えよう。米国においては、旧称DIS(Distributed Interactive Simulation)Workshopと呼ばれていたSimulation Interoperability Workshop[8]では分散環境下での異種シミュレータ統合の仕組みの標準化に関して議論を始めているが、これもつい最近の話である。
「だんだん遠くなる」の場合は種々のアルゴリズムは個別に提案されているものの、Direct (micro) simulation を直接的にサポートするような研究[9][10]はまだわずかのように見受けられる。
並列言語の研究は比較的盛んであるが、上記のような応用問題への橋渡しを行うもう一つのレイヤー、すなわち、並列処理用ミドルウエア(開発支援ツール、実行管理モニタ/スケジューラ、実行時ライブラリ等)の研究開発とその利用普及が相対的に遅れていると見られ、この分野に組織的に取り組むことは、技術発展だけでなく、新市場創出の可能性という意味でも大変有意義だと考える。

応用サイドに立つ時、高価で恐らく手間のかかる並列マシンをわざわざ利用する動機となるのは、多くの人が指摘しているように、『コスト』的に引き合う場合である。マシンを利用するための『コスト』としては、購入/レンタル価格(場合によっては開発費)、保守費、場所代、冷却も含めた電気代などの直接の費用の他に、プログラムの書き換えの手間や試行錯誤を繰り返す手間などが含まれる。
この『コスト』に引き合う理由をブレークダウンすることにより、どのような応用がペタフロップスマシン開発/利用のドライビングフォースとなるかが見えて来よう。そして、例えば並列処理ミドルウエアの研究開発を考える場合は、その方向が定まってくることが期待できる。
(1)倫理的理由
主に医療分野である。人体実験はもちろん、最近は動物愛護運動などの影響で動物実験さえ自由にならない場合がある。倫理的に許されない人体実験に相当するような医療行為で、計算機でのシミュレーションで代行できるものとして、仮想手術、仮想医薬品(複合/過)投与、配偶関係による遺伝的障害の予測などが挙げられよう。ただし、これらは人体モデル自身が十分に解明されていないため、10年後程度ではそれ程の進展はないかも知れない。なお、訓練としての手術シミュレーションだけは現在の技術でも十分可能と思われる。ただし、ペタフロップススケールの計算量は必要ないかも知れない。
(2)社会的理由
実験しようと思えばできないことはないが、それが社会的に許されないために、シミュレーションが望まれる一群の問題がある。例えば、環境汚染の進行予測、核実験、核兵器の保存条件と放射能漏れの危険性との関係、金融政策と株価変動などの経済問題などが挙げられよう。
(3)実現性の理由
実際に実験することができないために計算機上でシミュレーションを行わざるを得ないものもある。地球規模の環境変化(含む、汚染)予測、気象予測などが物理的な大きさの点で実験不可能である。時間スケール的に実験不可能な生命進化予測なども挙げられよう。なお、都市計画や大規模道路網における交通予測も実験は現実的とは言えず、シミュレーションが唯一の手段といえよう。
(4)費用・開発速度的理由
実験は技術的に可能であるし、昔は実際に実験を行なっていたが、現在は高速な計算機のお陰で、費用的にも、時間的にもシミュレーションが効率的であるという応用が沢山現れてきている。これらは産業界における開発競争という強い動機が作用しているために、今後もますます進展するのは確実である。
この範疇に入る代表例は航空機や自動車の空力特性解析、エンジン燃焼解析、LSI設計における論理合成、論理/故障シミュレーション、機械・構造の強度解析、熱伝導/放熱解析、などなど枚挙にいとまがない。訓練用シミュレータとしてはパイロット用のフライトシミュレータが老舗であるが、原子力発電所等の管制センタの操作員訓練シミュレータも、異常時に備えての訓練も可能なために一般的になってきているようである。
前節での考察は言わば仮想実験室(バーチャルラボ)としての並列マシン利用を想定して来たが、計算機にしかできないことを行う応用も出てきている。しかもビジネス分野での応用である。それは米国でこの3〜4年で急速に発展しつつあるデータマイニングである。
ディスクの価格低下と産業界の情報化の進展を背景に膨大なデータが蓄積されつつあり、その活用を動機としてデータマイニング技術とその応用が米国を中心として注目を集めている[11]。大量のデータの中から項目(または属性)間に隠された規則性を見つけ出し、それを経営・販売や製造プロセス改善に活かすことが目的であるが、データは今やテラバイト級に及び、ビジネス分野での大規模並列応用の本命の一つと目されている[12]。
従来の統計的手法による解析では、オペレータの勘や経験を元に、注目すべき複数項目を選択し、それらの相関などを求めたり、グラフ表示したりするということが行われてきた。知識発見を標榜するデータマイニングでは、項目の絞り込みを予め行わないことがポイントである。多数の項目間のそれぞれの組合せの検査はシステム側の責任であり、その組合せを旨く刈り込んで行くことがデータマイニングアルゴリズムの特徴となる[13]。
しかしながら、レコード数の増大により計算量が線形以上に増大するのはやむを得ず、レコード数をNとすると、良くてもO(N log N)程度の計算量が必要となる[12]。したがって、この部分がペタフロップスマシンの威力の発揮しどころとなる。多額の金銭に影響する経営方針の意志決定支援を用途とする場合は、例えばペタフロップスマシンの使用に数億円以上かかろうとも、その利用は促進されるであろう。
ペタフロップス(あるいはそのスケールの)マシンの将来について、そのシーズとニーズの両面から予測と分析を試みた。
シーズとしてはもちろん半導体デバイスの技術の進展もあるが、特に米国の世界一たらん政策的動機、フロンティア精神等の社会的風土が開発の促進剤として作用することが考えられる。良い面を評価する米国と異なり、平均点を判定基準としがちで、時には減点主義に陥る国民性を持つ日本は、ペタフロップスマシンだけでなく、その開発の陰で進展するであろう重要な技術さえも見逃す危険性を持っている。冷静な分析と多様性の確保を良しとする風土の醸成が望まれるところである。
ニーズとしては、バーチャルラボ的な応用が本命となり、特に費用・開発速度的な面でペタフロップスマシン利用が有利となるものが強力な原動力となるであろう。ただし、PE間通信が軽い探索型もしくはパラメータサーベイ的な応用でかつ規模がそれほど大きくないものについてはWS/PCクラスタがもっぱら利用されるため、ペタフロップスマシンの優位性はより大規模か、即時性の要求が強い応用に限られよう。また、大容量・高速マシン利用ならではのデータマイニング等の新しい応用も生まれつつあり、ペタフロップスマシンの陰に隠れて、例えば1世代前の枯れた技術となるであろうテラフロップスマシンの利用がどんどん広がっていく可能性も見逃せない。
仮想実験室の活用を思い浮かべれば分かるように、計算機を使いこなす力が技術力の差に現れる。実験精度を考えれば、単一のマイクロプロセッサではできなくて、並列マシンでこそできる実験が常に存在する。並列マシンを使いこなせるかどうかが一つのバリアになっているだけに、これを越えた者と越えない者には明確な差が現れよう。わが国は今回も米国が越えた後にロープを垂らして貰うのであろうか? それとも、組織力を動員して自力で、もしくは、国際的に協力しつつ這い上がるのであろうか?
<参考文献>
(福井義成委員)
PetaFlops計算機が必要な分野には、
のようなものがある。以下で詳細について説明する。
(1)ミクロな原理からマクロな現象を解明する場合
例えば、原子を支配する基本法則(第一原理)だけから物質の特性を計算して求める場合などがある。原子の基本方程式を対象とする原子数に対して計算し、そこから物質としての性質を求める分野である。
現在では原子レベルからの計算も計算機の能力からいろいろな仮定をおいて計算を進めることが多いが、それでは、仮定条件以外の答が出てくる可能性はない。なにも仮定をおかない第一原理からの計算ではこれまで人間が考えつかなかった答が出てくる可能性がある。この場合、扱える原子数がどれくらいかで扱える現象の範囲が決定する。例えば、1原子しか扱えない場合は、その原子が純粋な塊(多くの場合、結晶)でどの方向へも無限に続いている場合しか表現できていない。多くの有用な現象は、同じ原子が無限に続いている場合ではない(現実的にもそのようなことはあり得ない)。多くの場合、有用な現象は物質の表面や2つの性質の異なる物質の境界面でおきる。触媒の場合は物質の表面であり、半導体では2つの性質の異なる物質の境界面である。このような場合、小さな原子数しか扱えないと、出てくる現象は小さなものだけである。
現在の計算機の能力では、関係する原子の数が10〜100のオーダー程度が無理なく計算できる範囲である。1モルの分子数は1023のオーダーの原子数であり、その差は大きい。1023個の原子を扱うのは、現在は不可能である。すべての欲しい物質の性質を出すのには、1023のオーダーの原子数は必要はないが、現在の計算機の少なくとも1,000倍以上の能力は必要である。
(2)リアルタイム性が必要な分野のシミュレーション
シミュレーション結果のリアルタイム性が重要な分野では実時間よりも速くシミュレーション結果を得て、対応策を検討・適用するため、高速な計算機が必要になる。計算結果を得ることは現在の計算機でも可能であっても、リアルタイム性を実現するためには、PetaFlops計算機が必要になる場合であり、気象予測、地震予測、原子力発電所の制御などが考えられる。また、化学反応、溶鉱炉、半導体製造などで、製造段階の情報からシミュレ−ションを行い、結果を予測し、その後の工程を制御することにより、品質向上などが可能になる。
(3)多くのケ−スの計算が必要な場合
1ケ−スの計算にはペタフロップス計算機は必要ではないが、シミュレ−ションのケ−ス数が数千から数万ケ−スの場合がある。数多くの設計パラメータの組み合わせに対して性能の検証が必要な場合である。この場合、個々の計算ではPetaFlops計算機は必要ないが、数多くの計算結果をまとめるため、統合化されたシステムでないと不便である。
上記の用途以外でも、PetaFlops計算機は必要となると予測する。かつて、IBM7090やCRAY−1が出現した時、世界中で数台あれば、すべての計算が可能と言われてことがあったが、実際にはその予想をはるかに超える台数が使用された。これは高性能計算機が実現したことにより、当初想定していた用途以外にも新たな用途が出現したことを意味している。 PetaFlops計算機でも同じことが起こると考えられる。そのためには、多くの人に利用可能であり、アプリケーションから見て有用なものであることが重要である。
計算機のユ−ザが問題を解決するために計算機を使う場合、モデル(プログラム)記述が容易なことが大切である。ユーザにとって、演算が速いことではなく、解きたい問題が速く解けることが大切である。PetaFlops計算機でのモデル(プログラム)記述はどのようにするのが、望ましいのか?
ここでは、PetaFlops計算機は並列計算機と仮定する。現在、普通に使われている手続き型言語(Fortran、C燗凵jはノイマン型計算機を前提にしている。プログラム(モデル)はどのデ−タをどのように加工するかの手順を計算機に指示することにより構成されている。現在のアプリケーションも多くのものはアルゴリズムもノイマン型計算機を前提にしている。手続き型言語での並列プログラムの作成はユーザにとって負担が大きい。並列計算機では、単独プロセッサでは問題とならない複数プロセッサ間のタイミングの問題も生じる(図1)。タイミングにからむ問題は再現性が容易でないことが多く、これが手続き型言語での並列プログラミングの困難さの一因である。さらに、現在の並列計算機は各計算機ごとに性能を発揮させるための手法が異なっていることが多い。ユーザにとって、そのための負荷も大きい。
並列計算を使い易くするためには、並列計算機向きのモデル記述・アルゴリズムがあるべきである。ユーザにとって、手続き型言語で並列プログラムを書くには負荷が大きく、それが可能な人口は限られてしまう。その点からも並列処理のユーザを拡大するための障害になってしまう。デ−タ並列はベクトル化と本質的に同じであり、問題解決にはならない。
ユーザにとって、モデル記述が容易で、モデルの変更も容易で、なおかつ、並列性の抽出が計算機システムにとって容易であることが望ましい。
並列処理には非手続き型でモデル(プログラム)を記述する方法も解決のための1つの方策である。非手続き型言語とは、プログラムを手続きではなく、関数型ないしはオブジェクト指向的に因果関係だけを任意の順序で記述することである(図2)。関数型ないしはオブジェクト指向的な非手続き型言語で、並列プログラム(モデル)を記述することは人間の思考にあっており、非常に容易である。制御系でよく使用されるブロックダイアグラムが良い例である(図3)。

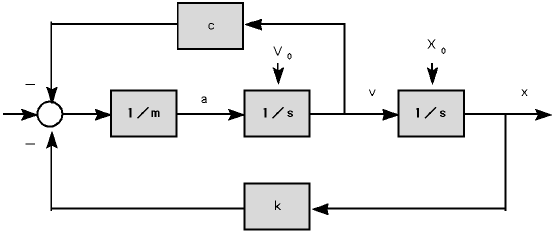
実例として、制御系でよく使用されている連続系シミュレーション言語の例を示す。連続系シミュレーション言語はブロックダイアグラムをそのまま計算機で記述することを目的としている。連続系シミュレーション言語はアナログ計算機と同じ発想である。
連続系シミュレーション言語はユーザが記述したモデルの演算順序を自動的に決定してくれる。連続系シミュレーション言語はノイマン計算機で、デ−タフロー計算機をシミュレ−ションしていると考えることができる。さらに、連続形シミュレ−ション言語では、各問題によって内容が異なるモデルの部分は、上記のような方法で容易に記述できる。さらに、常微分方程式の初期値問題を解く部分は共通化でき、共通化できる部分は各計算機の性能を十分発揮できるようにすることは困難ではない。(連続系シミュレ−ションは必ずしもPetaFlops計算機を必要としないことが多いが、非手続き型言語の例として使用した。)
例として、重りとバネから構成される振動子を考える。mを質量、kをバネ定数、cを減衰係数、xを物体mの変位、tを時間とすると、振動子は以下のような常微分方程式の初期値問題として記述できる。
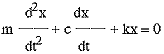
これを標準形式に変換する。vを速度、aを加速度とする。
さらに積分形式に変換する。x0はxの、v0はvの初期値とする。
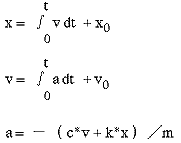
これを計算機に入力しやすいように、文法を定め、以下のように表現する。
この表現を連続系シミュレータの前処理を行うと以下のようなFORTRANに変換される。
| C C |
ZZ0002=V F=-K*X-C*V A=F/M V=INTGRL(ZZ0001,A) X=INTGRL(X0,ZZ0002) |
振動子の例は小さなものであるが、この例のようにモデル(プログラム)の記述が任意のところからできる言語であると、モデルの記述性が非常に向上する。手続き型言語ではモデルの計算順序を使用者が考慮しなければならず、小さなモデルでは可能であるが、大きなモデルでは不可能に近い。計算順序を間違えると位相ずれとなって現れる。
上記の非手続き型言語でのモデル記述も同じことであるが、並列化(高速化)のためには、ミクロなレベルではなく、よりマクロなレベルで記述できることが重要である。例えば、行列と行列の積を考える。手続き型言語(FORTRAN、C等)では
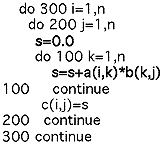
のようなループを記述することになり、計算機システムやコンパイラーは与えられたプログラムからベクトル化や並列化の可能性を抽出しなければならない(この例は非常に簡単なので問題にはならないが、実際の計算では非常に複雑な計算式となり、ベクトル化の可能性や並列性の抽出が容易ではない)。それに対して、行列と行列の積という記述を計算機に与えることができれば、計算機システムは並列化することは非常に容易になる。例えば、APL言語では行列演算が非常に簡単に記述できる。
マクロレベルでの問題記述をするため、別角度から計算の手順を考える。計算機でのシミュレーション手順(現象から計算結果の認識まで)を考えると図5のようになる。
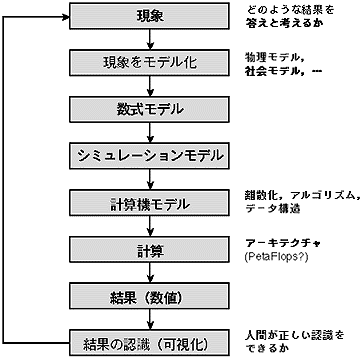
図5でPetaFlops計算機が有効なのは、計算の部分であり、計算を効果的に進めるためには計算の前後の作業が効率的に行われなければ、全体として良い結果は得られない。特に、Peta Flops 計算機で計算の部分が高速化されることにより、計算の前後の使い易さがますます重要になる。PetaFlops 計算機の性能を十分発揮させるためには、上位レベル(マクロなレベル)での工夫が重要である。以下で簡単な例を示す。
この例は残念ながら並列処理の例ではなく逐次処理の例である。しかし、マクロなレベルで問題を記述することにより、並列処理も問題の並列性を抽出し易くなり、計算機ごとの特性も利用し易くなる(専用ライブラリの整備などで実現)ことは逐次処理も並列処理も同じである。一般的に高速化のレベルを考えると、以下のようになる。
上記の各部分に対応する高速化の工夫をするとどのような効果があるかを簡単な例(下記)で示す。
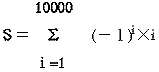
最も単純にプログラムを作成するとプログラム1のようになる。
計算の中で冪乗を計算しないように工夫するとプログラム2のようになる(1を適用)。この工夫では約4倍速くなっている。
さらにル−プ内での乗算を避ける工夫をするとプログラム3のようになる(1を適用)。この工夫の効果は約5倍であり、プログラム2と比べて約1.25倍速くなっている。
元々の問題を良くみると、計算結果はプログラム4のような簡単な式で計算できることが分かる(3を適用)。これを実行するとプログラム1に比べて、約9,000倍も速く計算できる。
計算速度比は、あるスカラ−計算機の場合、下記のようになる。
| プログラム | |
| 1 | 1 倍 |
| 2 | 4.06 倍 |
| 3 | 5.06 倍 |
| 4 | 9,606.16 倍 |
この例は非常に簡単な例であるが、プログラムレベルでの高速化はドラステックな改善は不可能であり、ドラステックな高速化はアルゴリズムの変更、モデル化の変更等でなければ不可能であることを示している。図5の上の方へ行くほど、その効果は大きい。そのためには、モデル(プログラム)のマクロレベルでの記述が必要になる。
PetaFlops計算機を使用するであろうユ−ザが本質的(直接的)に欲しいものは下記のようなものである。
これを実現するためには、PetaFlops計算機のような速い計算機とモデル(プログラム)記述手法(非手続き型、マクロレベルなど)の変更とPetaFlops計算の前後の処理の高速化・高度化である。前後の処理の高速化・高度化には数値的処理だけではなく、非数値処理の高速化・高度化、認識(せまくは可視化)の高速化・高度化も重要である。
また、PetaFlops計算機が実現すると、現在、想定しているた用途以外にも新たな用途が必ず出現する。それは過去の例が実証している。そのためには、PetaFlops計算機が多くの人に利用可能となり、アプリケーションから見て有用なものであることが重要である。
<参考文献>
(横川三津夫委員)
ここ数年、未知現象の解明や実験不可能な現象の解明、大規模構造物等の詳細な解析等を行うために、数値シミュレーション技術を駆使して研究を行う、理論、実験につぐ「第3の科学」と称される計算科学が注目を集めている。計算科学の進展は、単体プロセッサの高速化、主記憶装置の大容量化、コンパイラなどソフトウエア技術の発展などの計算機技術の発展によってもたらされている。
しかし、現在よりもさらに大規模な問題や、より詳細な解析を行うためには、複数の計算プロセッサをネットワーク結合した並列計算機を用いるのが唯一の解決法と考えられる。現在の並列計算機の動向を見ると、MIMD型のものが主流になっているが、そのプロセッサ・アーキテクチャやメモリ配置を見ると、商用化された並列計算機の種類は千差万別といっても過言ではない。このため、いろいろなサイトに並列計算機が導入されている現状においても、並列計算機の使用方法は未だ確立されていない。ある種の計算を行っていくときに、計算の流れを順序立てて考えれば良かった逐次型計算機やベクトル型計算機を、解析の道具としてきた応用分野の研究者・技術者が、それぞれのアプリケーション問題を解く場合、どういう並列計算機アーキテクチャの上で、どういうプログラミングを行ったらよいかという問題に対する決定的な指針は与えられていないのである。
従来用いているプログラムをそのまま並列計算機で並列実行できないことはもとより、一所懸命手作業で並列化しても、多くの分野の問題でその計算機能力を十分に引き出せないことが分かってしまった。ただ単に、カタログ性能値(理論ピーク性能値)が高いということだけで、アプリケーション・プログラムが高速に実行できるという幻想は脆くも崩れたのである。自動並列化コンパイラが開発段階にある現状では、コンパイラによる高速化の望みもない。今のような状況が続けば、ペタフロップス計算機が開発されたとしても、その性能の1%も発揮できないであろう。
少なくともペタフロップス計算機の開発が始まるまでには、アプリケーション問題や数値シミュレーション手法、そのカーネルとなる計算アルゴリズム等に対して、なんらかの並列計算モデルを構築し、最も適合する並列計算機のタイプや、その並列計算機の上での並列化方法等の技術を検討、蓄積しておく必要がある。そして、応用分野の研究者・技術者に並列化技術を正しく提示することができれば、並列計算機がより有効に使われ、ペタフロップス計算機開発の機運が高まることであろう。
アプリケーション・プログラムの並列化では、計算処理やデータのプロセッサへのマッピングが重要な問題である。ここでは、並列計算を行うときのデータアクセスパターンや演算処理の方法等を分類することを考えてみる。
いろいろなアプリケーション問題の並列計算モデルへの分類については、問題やそれを解くために用いられるアルゴリズムに内在する並列性を、いくつかのモデルで表現することが試みられている。Pancake[1]は、アプリケーション問題を並列処理するときの実行形態を問題アーキテクチャ(problemarchitecture)と呼んで、4つに分類した。
科学技術分野の多くのアプリケーション問題では、非定常現象の時間発展シミュレーションを行うことが多く、計算処理全体を見た場合にはfully or loosely synchronous parallelismに分類される。
数々の数値シミュレーション手法の並列化の経験から、時間発展シミュレーション問題の分類では、Pancakeの分類が並列計算モデルとして十分な表現能力がないことが明らかである。1時間ステップ内の計算処理に対して、データのアクセスパターンやデータ転送パターンを考慮した並列計算モデルを考える必要がある。そこで、1時間ステップ内のデータアクセスパターンと、データ転送パターンという観点で以下のモデルを考えた。
ここで、RALC、RAGCは、規則的にデータアクセスを行う手法のモデルであるため、ベクトル演算器をもつプロセッサに良く適合する。IALC、IAGCは、スカラ並列計算の方が望ましいモデルである。時間発展の各時間ステップは、各プロセッサで一致させる必要があるので、バリア同期を取る必要がある。
表1に、流体計算に用いられる4つの数値シミュレーション手法と分子動力学法を並列計算する場合に、ベクトル計算適合性と領域分割による並列化の時のデータ通信パターンという観点で分類したものを示す。これらの手法の並列計算モデルも同時に示す。有限差分法と格子ボルツマン法は、同じ並列化手法を用いることができ、同じ計算モデルRALCに分類される。DSMC法では、粒子が計算領域全体に移動する可能性を持っているので、全プロセッサが通信対象となる。
| ベクトル 計算適合性 |
領域分割による並列化時の 通信パターン |
並列計算 モデル | ||
| 有限差分法 | ○ | 隣接プロセッサ間 | 規則的 | RALC |
| スペクトル法 (フーリエ法) |
○ | 全プロセッサ間 | 規則的 | RAGC |
| DSMC法 | × | 全プロセッサ間 | 不規則的 | IAGC |
| 格子ボルツマン法 | ○ | 隣接プロセッサ間 | 規則的 | RALC |
| 分子動力学法 (短距離力) |
× | Cut-Off距離内にある プロセッサ間 |
規則的 | IALC |
わずか5つの数値シミュレーション手法に対しても、適合する計算機のタイプが違うことを考えれば、ペタフロップス計算機もアプリケーション問題に応じて開発されることになるであろう。
ペタフロップス計算機を必要とする大規模数値シミュレーションにおいては、
の3つのケースが考えられる。
(1)のケースでは、各パラメータに対して最終的に得られた結果を統合、整理するための処理方法を考える必要があるものの、プロセッサ数が多ければ、大量のケースの数値シミュレーションが同時に実行可能であるので、超並列計算機が極めて有効である。例えば、大気モデルを用いた気象予測のような非線形現象では、いくつかの異なった初期状態から計算を開始し、結果の集合平均をとった確率的な結果が重要な意味を持つ。この場合には、一つ一つのパラメータに対して計算時間が多くなったとしても、完全並列の計算ができるので、高い実行効率が得られる。
(2)のケースでは、時間方向の並列性を見い出し計算時間を短縮することが考えられる。通常、非定常時間発展の数値シミュレーションでは、時間微分に関して微小時間 Δt で離散化し、時刻 t0 の計算領域の値を用いて、時刻 t0+Δt の値を求めているが、計算が時系列的に順序正しく実行することを保証をするために、1時間ステップ毎に計算の同期を取らなければならない。このため、時間方向の並列性は期待できず、長時間現象の数値シミュレーションの短縮は、1時間ステップ内の計算時間を短くするしかない。しかし、空間的な離散点の数が少ない場合、すなわち1時間ステップ内の計算量が少ない場合は、並列計算による速度向上は望めない。計算量が少なければ高い並列度は得られないため、プロセッサ数を増加させてペタフロップス計算機を構成する方法は意味を持たない。
(3)のケースは、詳細な数値シミュレーションを行うか、計算領域を大きくする場合である。1時間ステップ内の計算において、高い並列化効率が得られることが分かっているならば、並列度を大きくすれば時間短縮が図られる可能性がある。しかし、総演算量が増えているから、全体の経過時間は変化なく、詳細な結果が得られるまでの実時間は変わらない。
以上の結果から、大粒度の並列化を確保しつつ、プロセッサ間の通信性能と計算性能のバランスの取れた数値シミュレーションが並列化効率を保つ上で必要である。また、計算形状が比較的単純な理学的シミュレーションと、実用問題を考える工学的シミュレーションでは、大分状況が異なることも考慮しておく必要がある。
数値シミュレーションの問題点を2つ挙げておきたい。まず、計算誤差の問題である。離散化の精度を上げていくと、打切り誤差よりも丸め誤差が優位になっていくのはよく知られた事実である。偏微分方程式の時間微分項を、数値積分する時の誤差の議論は、その刻み幅が小さくなるほど、丸め誤差が顕著になることが分かっていても、定量的な評価があまりなされていない。計算機性能が向上して、単に離散化格子を増加させる傾向にあるが、さらに詳細な解析をするためには浮動小数点数の表現桁数を多くするなど、根本的なアーキテクチャの変更が必要になると思われる。
もう1つは、数値シミュレーション結果の取り扱いに関する問題である。すでに知られている現象を、数学モデルを改良したり、数値シミュレーションの精度を向上させたり、また多くの観測データ等を初期、境界条件とすることにより、再現することは可能と思われる。ペタフロップス計算機が開発されれば、かなりの現象が数値シミュレーションによってとらえることができるであろう。
しかし、実験や観測によっても検証不可能な現象に対して数値シミュレーションする場合、数値シミュレーションに用いられた数学モデルが本当に正しいと誰が保証できるのだろうか。また、すべての要因を数学モデルで考慮してないために、予測できない事象が起こりうる可能性を誰が否定できるのだろうか。不十分なモデルによって得られた数値シミュレーション結果を、ペタフロップス計算機で計算したという理由だけで、その結果が一人歩きして使われてしまうことがないように、数値シミュレーション結果の取り扱いについては、十分議論する必要がある。
ペタフロップス計算機が出現する頃には、ピーク性能によって計算機の性能を定義する悪習はなくなっていると思う。プロセッサをたくさん並べるだけのペタフロップス計算機では、多くのアプリケーションの実効性能は数10テラフロップスも達成できない。また、Embarrassingly Parallel に属するアプリケーション問題に対して、ペタフロップスの性能を達成したといっても、それは簡単な並列計算が可能であるから、これでペタフロップス計算機というのは不適切だろう。したがって、計算機の実効性能の評価方法を確立する必要があり、やはりアプリケーションごとの実効性能でペタフロップスと称するのがいいのではないだろうか。
さて、科学技術計算用のペタフロップス計算機は本当に必要なのだろうか。研究者や技術者、特に理学的な計算科学研究をしている研究者は、再現なく計算性能を求めている。しかし、ペタフロップス計算機が普及機とならない限り、その開発費は数兆円を越えるものと思われ、開発するならば国主導の開発体制、資金の調達が必要であろう。誰もが納得する適用応用分野が見つけられないうちは、ペタフロップス計算機開発のモチベーションは薄い。
<参考文献>